The filter is a very useful function that can help us eliminate bad tickets. SamLotto Lottery Software supports 50 base filters. Over 90% of filtering methods not available in any other lottery programs. that is so easy to use that You don’t even need to know how they work of each filter. For advanced filters conditions, please visit here.
The program can automatically generate the filter condition parameters, no need to set the filter condition parameters manually, it is all done automatically by the program.
For more information on how to use the filters and how to set the filter condition parameters please refer to our other articles.
This article focuses on the filtering algorithm of each filter.
Next, we will detail each filter.
Table of Contents
1. Odd Count
Determines how many odd numbers can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Odd Count?
Count all the odd numbers in the number combination.
For example: 06 11 17 18 21 31 45, the Odd numbers: 11 17 21 31 45, so Odd Count=5.
2. Even Count
Determines how many even numbers can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Even Count? Count all the even numbers in the number combination.
For example: 06 10 17 18 21 31 45, the even numbers: 06 10, so Even Count=2.
3. High Count
Determines how many high numbers can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate High Count?
All numbers are divided into two groups, The groups are 1 to 34 (low numbers) and 35 to 69 (high numbers) for Powerball (1 to 69 numbers).
For example: 04 19 23 25 49, the high numbers: 49, so High Count=1.
4. Low Count
Determines how many Low numbers can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Low Count?
All numbers are divided into two groups, The groups are 1 to 35 (low numbers) and 36 to 70 (high numbers) for Mega Millions (1 to 70 numbers).
For example: 04 05 17 43 52, the high numbers: 04 05 17, so Low Count=3.
5. Prime Count
Determines how many Prime numbers can occur in a combination, If the combination does not match the set conditions will be filtered out.
What is a Prime number?
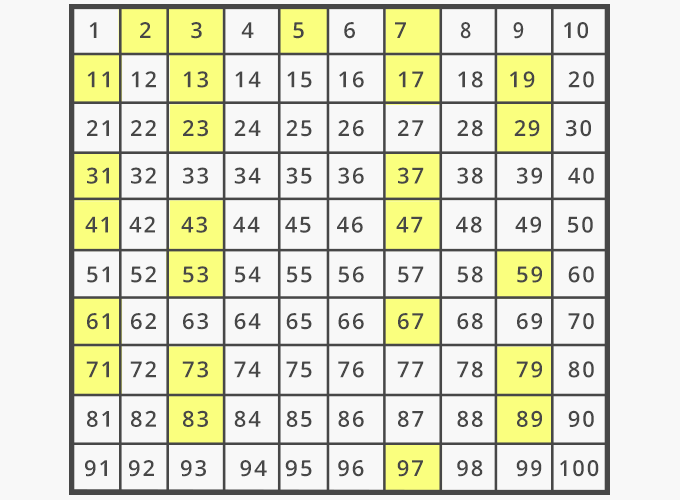
Prime numbers are numbers that have only 2 factors: 1 and themselves. For example, the first 5 prime numbers are 2, 3, 5, 7, and 11. By contrast, numbers with more than 2 factors are called composite numbers. Created by Sal Khan.
Here’s a list of all the prime numbers up to 100, marked in yellow.
For example: 02 11 17 20 21 31 42, the Prime numbers: 02 11 17 31, so Prime Count=4.
6. Number Sum
Determines the sum value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Numbers Sum?
The value of the sum of all numbers in the combination.
For example, 05, 11, 14, 15, 22, 39, the sum is 5+11+14+15+22+39=106, so Number Sum=106.
7. Average Value
Determines average value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate the average value of the numbers?
Add the numbers in the combination to each other. then divide by amount.
For example, 05, 11, 14, 15, 22, 39 sum = 5+11+14+15+22+39=106, so average value is 106/6=17.
8. Unit Number Sum
Determines Unit Number Sum value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Unit Number Sum?
Add the SECOND digit numbers in the combination to each other.
What is the Unit Number?
The second digit of a number, for example, 01, 09, 14, 15, 22, 39 the end unit numbers is: 1, 9, 4 5, 2, 9
For example, 03, 07, 19, 21, 42, 59, Unit Number Sum is 3+7+9+1+2+9=31, so Unit Number Sum=31.
9. Unit Number Different Number
Determines Unit Number Different Number amount can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Unit Number Different Number?
Count all Unit Numbers, remove duplicate numbers, and count the amount.
What is the Unit Number?
The second digit of a number, for example, 01, 09, 14, 15, 22, 39 the end unit numbers are 1, 9, 4 5, 2, 9
For example, 03, 07, 19, 21, 42, 59, Unit Number 3, 7, 9, 1, 2, 9, Different Number 3, 7, 9, 1, 2 so Unit Number Different Number=5.
10. Successive
Determines Successive numbers amount can occur in a combination, If the combination does not match the set conditions will be filtered out.
What is the successive number?
Count all adjacent numbers in a combination and find the group with the highest amount of adjacent numbers.
For example 03 04 25 26 27 43, 03 04 and 25 26 27 are all the successive numbers, 03 04 adjacent amount is 2, and 25 26 27 adjacent amount is 3, so Successive=3.
11. Successive Groups
Determines Successive Groups amount can occur in a combination, If the combination does not match the set conditions will be filtered out.
What is successive number groups?
Count all adjacent numbers in a combination and find the group amount of adjacent numbers.
For example 03 04 25 26 27 43, 03 04 and 25 26 27 are all the successive numbers, 03 04 is a group and 25 26 27 is a group, so Successive Groups=2.
12. Odd Successive
Determines Odd Successive numbers amount can occur in a combination, If the combination does not match the set conditions will be filtered out.
What is Odd successive number?
Count all odd adjacent numbers in a combination and find the group with the highest amount of odd adjacent numbers.
For example 03 13 25 26 27 43, 03 13 25 and 27 43 are all the odd numbers, 03 13 25 adjacent amount is 3, and 27 43 adjacent amount is 2, so Odd Successive=3.
13. Even Successive
Determines Even Successive numbers amount can occur in a combination, If the combination does not match the set conditions will be filtered out.
What is Even successive number?
Count all even adjacent numbers in a combination and find the group with the highest amount of odd adjacent numbers.
For example 04 12 22 25 33 43, 04 12 22 are all the even numbers, the adjacent amount is 3, so Even Successive=3.
14. Minimum Number
Determines smallest number can occur in a combination, If the combination does not match the set conditions will be filtered out.
For example, 03 15 17 29 41 45, the smallest number is 03.
15. Maximum Number
Determines Maximum number can occur in a combination, If the combination does not match the set conditions will be filtered out.
For example, 03 15 17 29 41 45, the maximum number is 45.
16. First-Last Distance
Determines First-Last Distance value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate First-Last Distance value?
The value of the difference between the last number and the first number.
For example 11 15 17 30 41 51, the last number is 51, the first number is 11, so the First-Last Distance value is 51-11=40.
17. Max Distance
Determines Max Distance value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Max Distance value?
The values of the difference between the all adjacent two numbers. the largest value is Max Distance.
For example 02, 05, 17, 19, 27, 31, the distance list : 3 (05-02=3), 12 (17-05=12), 2 (19-17), 8 (27-19), 4 (31-27=4), so the max distance is 12.
18. Average Distance
Determines Average Distance value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate the Average Distance value?
The values of the difference between the all adjacent two numbers, all values are added together and finally divide by the numbers amount.
For example, 02, 05, 17, 19, 27, 31, the distance is 3 (05-02=3), 12 (17-05=12), 2 (19-17=2), 8 (27-19=8), 4 (31-27=4). (3+12+2+8+4)/5=5, so the distance average value is 5.
19. Different Distance
Determines Different Distance amount can occur in a combination If the combination does not match the set conditions will be filtered out.
How to calculate Different Distance?
The values of the difference between the all adjacent two numbers, remove duplicate values, and count the amount.
For example: 02, 05, 08, 19, 27, 31, the distance is: 3 (05-02=3), 3 (08-05=3), 11 (19-08=11), 8 (27-19=8), 4 (31-27=4), remove duplicates value 3, so the different distance is 4.
20. AC
Determines AC value can occur in a combination, If the combination does not match the set conditions will be filtered out.
What is AC value?
AC value called Arithmetic Complexity value is a value which is calculated to determine the variation of differences among all numbers in one lottery combination.
For more information about AC value filter, please see our other articles.
21. Same Last Drawn
This filter Count of the numbers repeats found in the previous draw winning combination. If the combination does not match the set conditions will be filtered out.
You can specify an drawn as the last drawn, the default is the last drawn. As shown below:
22. Sum Value Even Odd
Determines Sum Value Even or Odd can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Sum Value Even Odd?
Add the numbers in the combination to each other, we will get the sum value, if this value is an odd number, the value is 1 for this filter, if this value is an even number, the value is 0 for this filter. So this filter has only two values: 0 or 1.
For example 10 17 18 21 31 45, the sum of this line is 142, 142 is an even number, so Sum Value Even Odd is 0.
23. Unit Number Group Count
Determines Unit Number Group can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate groups of units are there in a winning line?
For example, Please check the table below, 10 17 18 21 31 45, so here we have 3 groups of winning unit numbers, one group of unit =the green shaded area see below. Units 0 and 1 are next to each other so they are in one group, unit 5 is alone, so another group and finally units 7 and 8 are next to each other so they form one group- the third group, so all together we have 3 groups of winning units.

24. Decade Group Count
Determines Decade Group can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Decade Group?
From 0 – 9, we call this a decade of 0
From 10-19, it is called a decade of 10
From 20-29, it is called a decade of 20
From 30-39, it is called a decade of 30
And so on, until the decade of 90 which is from 90-99, for a 6/45 game we have only 5 decades.
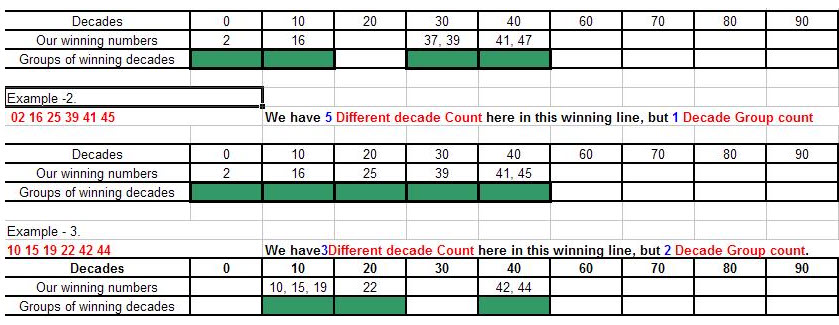
Let us take our winning line as 02 16 37 39 41 42, we illustrate this line in the table as below:

As you can see, here we can count only 2 groups of decades. A group of decades = a shaded area. Decades 0 and 10 are next to each other, so they form one group. Also, decades 30 and 40 from one group because they are next to each other.
25. Different Decade Count
Determines Different Decade can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Different Decade?
Example: 02 16 37 39 41 45 We have 4 Different decade Count here in this winning line, but 2 Decade Group count.
26. Same End Units with Last Drawn
This filter allows you to specify how many of the numbers selected repeat an end unit number found in the previous draw’s winning line. If the combination does not match the set conditions will be filtered out.
You can specify an drawn as the last drawn, the default is the last drawn. As shown below:
27. High Units Count
Determines High Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate High Units?
We have 10 units in lottery ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9). These units can be first units or end units in a number. In this filter, we will use only the last four units as high units (6, 7, 8, and 9). We consider ONLY the Second Unit in a lottery number. The filter counts how many of these (High Units) are in the winning line. The filter also counts repeating units.
Example:
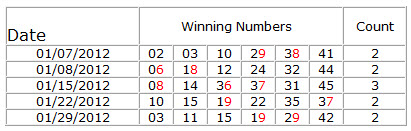
28. Odd Units Count
Determines Odd Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate High Units?
Odd Units from 0-9 are: 1, 3, 5, 7, 9. So there are only 5 Odd Units.
See the table below for details on how to calculate Odd Units.
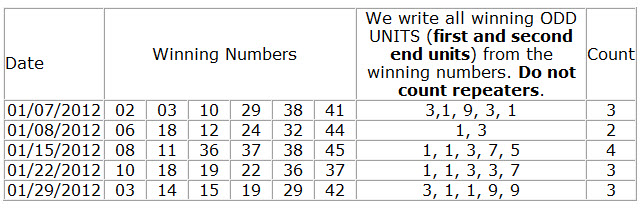
29. Lowest 4 Units Count
Determines Lowest 4 Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Lowest 4 Units?
We consider only these Units as lowest: 1, 2, 3, 4. Do not use the zero units. So there are only 4 units to be used in our Filter.
See the table below for details on how to calculate Lowest 4 Units.
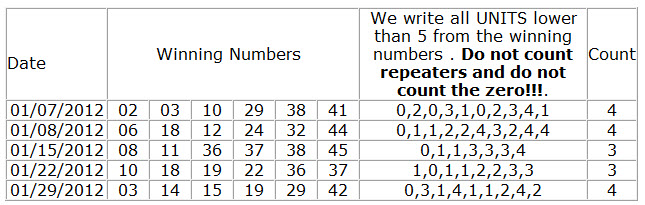
30. Successive Paired Units Count
Determines Successive Paired Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Successive Paired Units?
We have 10 units in a lottery ( 0, 1,2,3,4,5,6.7.8.9). We pair them into successive pairs of units: 01, 12, 23, 34, 45, 56, 67, 78, 89. Our filter will count ONLY from these numbers.
See the table below for details on how to calculate Successive Paired Units.
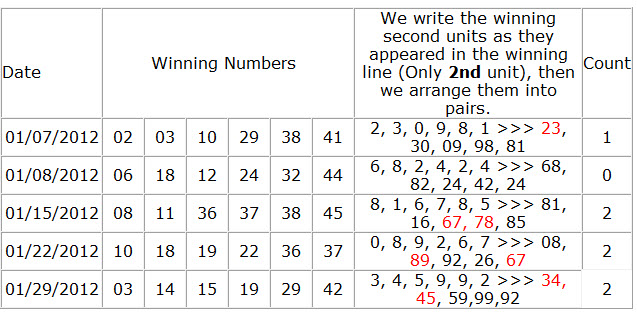
31. Pairs Count Odd and Even Units
Determines how many Pairs Count Odd and Even Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Pairs Count Odd and Even Units?
Only a number with both Odd and Even units is counted. Example of paired units Odd and Even together: 01, 03, 05, 07, 09, 10, 12, 14, 18, 21, 23, 25, 27, 29, 30, 32, 34, 36, 38, 41, 43, 45, 47 and so on. This filter uses ONLY these numbers to find pairs in a winning line with both Odd and Even units.
See the table below for details on how to calculate Pairs Count Odd and Even Units.

32. InterChangeable Units Count
Determines InterChangeable Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Pairs Count Odd and Even Units?
Every lottery number contains 2 units, first and second unit, if we change their positions then we get a new number, this new number must not be bigger than the biggest number in your lottery game. Example: number 34 (The first unit is 3 and the second unit is 4) we can change unit positions to 43 and the new number is still less than 45 in the 6/45 lottery. Other possible interchangeable numbers for 6/45 lotto include: 01, 02, 03, 04,10, 12, 13, 14, 20, 21, 23, 24, 30, 31, 32, 34, 40, 41, 42, 43. So there are 20 numbers in the 6/45 lotto game, this filter uses these numbers to find winning numbers which its unit positions can be interchanged. Do not include the numbers: 11, 22, 33, 44…
See the table below for details on how to calculate InterChangeable Units Count.
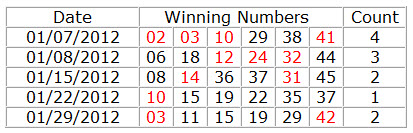
33. Count for 1 2 3 Units
Determines how many Count for 1 2 3 Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Count for 1 2 3 Units?
The most drawn units in any winning line e.g 6/45 is unit 1, unit 2, and unit 3.
This filter counts these units in a winning line including repeaters.
See the table below for details on how to calculate Count for 1 2 3 Units.
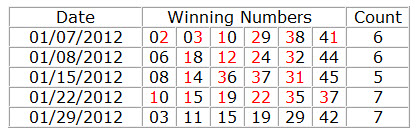
34. Even Units Count
Determines how many Even Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Even Units?
Even Units from 0-9 are: 0,2,4,6,8. Do not use zero. So there are only 4 Even Units to be used in our Filter: 2, 4, 6, 8.
See the table below for details on how to calculate Even Units.
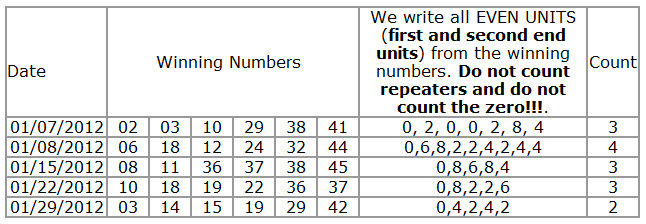
35. Pairs Count Even Units Only
Determines how many Pairs Count Even Units Only can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Pairs Count Even Units Only?
Both units are Even. Example of Even pairs: 02,04,06,08,20,22,24,26,28,40,42,44, ..Zero is included because it is an Even unit. The filter counts the number of Even pairs in a winning line.
See the table below for details on how to calculate Pairs Count Even Units Only.
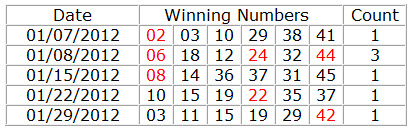
36. Pairs Count for 1 2 3 Units
Determines how many Pairs Count for 1 2 3 Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Pairs Count for 1 2 3 Units?
Example: 11, 12, 13, 22, 23, 31, 32, 33. The filter counts the number of pairs made with 1, 2, and 3 in a line.
Details on Pairs Count for 1 2 3 Units.
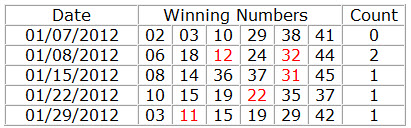
37. Successive End Units
Determines how many Successive End Units can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Successive End Units? We have 10 units in a lottery ( 0, 1,2,3,4,5,6.7.8.9). These units can be first units or second end units in a number. Example: number 34 (The first unit is 3 and the second unit is 4). In this filter, we will count only the second units for the successive count.
Details on Successive End Units.
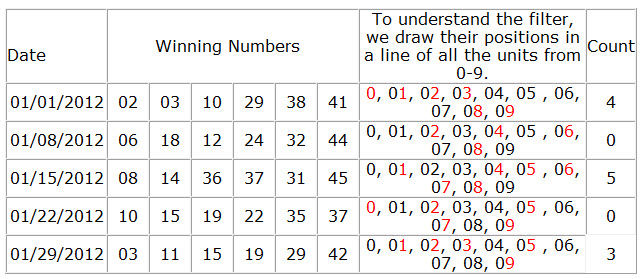
38. Pairs Count Odd units Only
Determines how many Pairs Count Odd units Only can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Pairs Count Odd units Only?
Both units are Odd. Example of Odd pairs: 11, 13, 15, 17, 19, 31, 33, 35, 37, 39, 51, …Zero is not counted because it is an Even unit. This filter counts the number of pairs in a winning line.
Details on Pairs Count Odd units Only.
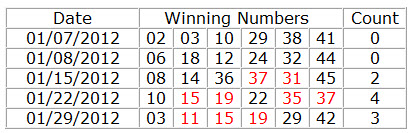
39. Units (0) Number Count
Determines how many 0-digit can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to count 0-digit?
We split all the numbers into two numbers, for example, 03 11 15 19 42 can be split into 0, 3, 1, 1, 1, 5, 1, 9, 4, 2. count all first and second end digit equal to 0. If the number is less than 10, the first unit is 0.
The following table shows how to count Units (0) Number.
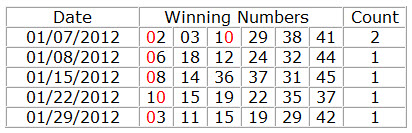
40. Units (1) Number Count
Determines how many 1-digit can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to count 1-digit?
We split all the numbers into two numbers, for example, 01 12 25 36 59 can be split into 0, 1, 1, 2, 2, 5, 3, 6, 5, 9. count all first and second end digit equal to 1.
The following table shows how to count Units (1) Number.
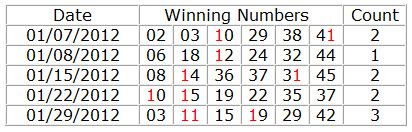
41. Units (2) Number Count
Determines how many 2-digit can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to count 2-digit?
We split all the numbers into two numbers, count all first and second end digit equal to 2.
The following table shows how to count Units (2) Number.
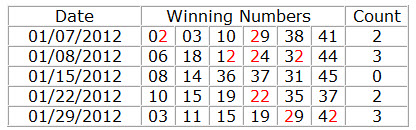
42-48 Filters
And so on, 42 to 48 filters are similar to Units (0) Number Count, Units (1) Number Count, Units (2) Number Count. About Filters Units (3) Number Count, Units (4) Number Count, Units (5) Number Count, Units (6) Number Count, Units (7) Number Count, Units (8) Number Count, and Units (9) Number Count, Please refer to the previous 3 filters.
49. Root Sum
Determines the Root Sum value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate numbers Root Sum value?
Add the numbers in the combination to each other, then split the sum value and add all the digits together again.
For example, 08 13 14 33 35 40, the sum of this combination is 143 and the Root Sum is 1+4+3=8, so the Root Sum value is 8.
For more calculation examples, please see the table below.
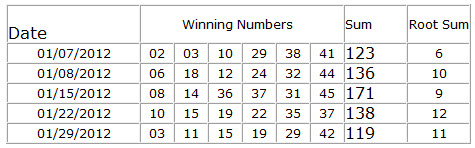
50. First and Second Unit Sum
Determines First and Second Unit Sum value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate First and Second Unit Sum value?
All the numbers in the combination are broken down into two digits (Position 1 is called the FIRST digit and position 2 is called the SECOND digit), and then all the digits are summed.
For example, 01 08 14 29 31 42, Sum of first digit is 0+0+1+2+3+4=10, and Sum of second digit is 1+8+4+9+1+2=25. Sum of first units + Sum of second units equals 10 + 25, so First and Second Unit Sum value is 35.
51. Min Distance
Determines Min Distance value can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Min Distance value?
The values of the difference between the all adjacent two numbers. the minimum value is Min Distance.
For example 02, 05, 17, 19, 27, 31, the distance list : 3 (05-02=3), 12 (17-05=12), 2 (19-17), 8 (27-19), 4 (31-27=4), so the minimum distance is 2.
52. Composite Count
Determines how many Composite numbers can occur in a combination, If the combination does not match the set conditions will be filtered out.
How to calculate Odd Count?
Count all the odd numbers in the number combination. For example: 03, 11 12, 14, 42. Composite numbers: 12, 14, 42, so Composite Count is 3.
What is Composite Number?
A composite number is an integer greater than 1 that is not a prime number, meaning it can be divided by other integers besides 1 and itself. For example, 4 is a composite number because it can be divided by 2 and 4, but it is not a prime number.
There are many composite numbers within 90, such as 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, and 90.
Summary
The above is a detailed introduction to all the base filters, if you want to know how to use the filter please check our other articles.
If you are interested in our filtering methods, you can download and use the free version of SamLotto lottery software, The free version allows you to use the first 5 filters: Odd Count, Even Count, High Count, Low Count, and Prime Count.